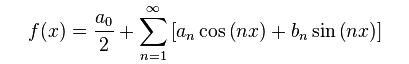Kaum ein anderes mathemathisches Verfahren ist für KlanggestalterInnen von ähnlich grundlegender und umfassender Bedeutung wie die Fourieranalyse[1] . Dieses Analyeseverfahren ist die Grundlage für viele Geräte / Plug-Ins und Messgeräte, für spezielle Filteranwendungen, Hallgeräte und vieles mehr. Fast alle Bereiche der Klanganalyse nutzen die Fourieranalyse als Grundlage, sei es die Balkenanzeige des Klangspektrums (wie vielen Analyzern, siehe auch noch die FFT, die Fast Fourier Transormation), die Analyse von Räumen (Raumakustik) und die sog. Entzerrung von Lautsprechern und Abhöranlagen, die Berechnung von Filterkurven oder die Analyse von unterschiedlichsten akustischen Anforderungen oder Gegebenheiten.
Auch für so wichtige Applikationen wie das Denoising, Decrackling, Declipping oder Declicking ist das Verstehen der grundlegenden Funktionen der Fourieranalyse von grundlegender Bedeutung und kann kaum überschätzt werden.2
Von zusätzlicher praktischer Bedeutung ist ausserdem, dass das Verstehen der Funkionsweise mancher Programme / Plug-Ins / Geräte auch zu einer besseren und sinnvolleren und damit auch qualifizierteren Anwendung führen wird; und daraus wiederum bessere Ergebnisse resultieren können.
Aufgrund der enormen Bedeutung und des hohen Erkenntnis- und Verständnisgewinns sollte man sich nicht von der Komplexität der Fourieranalyse abschrecken lassen. Ausserdem sollen hier keine mathematischen Berechnungen durchgeführt werden – vielmehr ist es das Ziel, die Fourieranalyse und deren Konsequenzen für die Klanganalyse und vor allem der Klanggestaltung oder Klangsynthese und deren Bedeutung beim Einsatz von Applikationen (z.B. Denoising, Declicking oder IR-Reverb/Convolution-Reverb) zu begreifen.
[work in progress…]
links:
Fourieranalyse, Fouriertransformation, Disktrete Fouriertransformation, Lineare zeitinvariante Systeme, Fouriertransformation pdf der TUHH, Fouriertransformation/Faltung pdf, Fourier-Reihen pdf, FFT (fast Fourier transform) oder die FFT in englisch (interessant, wie verschieden die beiden Texte sind)
links zu Videocasts und mehr:
iTunesU:
umfangreiches Kursmaterial von der Stanford-University
https://itunes.apple.com/de/course/fourier-transform-its-applications/id495052537
https://itunes.apple.com/de/podcast/lecture-6-notes-fourier-transform/id413140966?i=96466620&mt=2
oder von der University of Arizona
https://itunes.apple.com/de/itunes-u/opti512r-linear-systems-fourier/id413140966?mt=10
oder von der Open University
https://itunes.apple.com/de/itunes-u/fourier-series-for-ipod-iphone/id380228082?mt=10
auf YouTube bzw. YouTubeEDU:
http://www.youtube.com/watch?v=1JnayXHhjlg
http://www.youtube.com/watch?v=x04dnqg-iPw
http://www.youtube.com/watch?v=ug9Co75tQuo
Diese links dienen nur als Einstieg – für Interessierte gibt es diesbezüglich noch sehr viel zu entdecken!
Literatur:
Sucht man online nach Literatur zu diesem Thema ist die Auswahl ungewöhnlich groß, was auch die Bedeutung der Fourieranalyse deutlich macht. Nur nebenbei sei erwähnt, dass dieses Verfahren auch für Astronomen (z.B. zur Analyse des Schwingungsverhalten von Sternen) oder für Chemiker von Bedeutung ist; bei einem Buchkauf sollte man also darauf achten, für welche Zielgruppe das Buch verfasst wurde.
Zudem bietet auch google-books u.a. Informationen.
[work in progress…]
1 speziell die englische Wikipedia erklärt die Fourier-Reihen (Fourier Series) sehr anschaulich, gut verständlich und mit vielen animierten Graphiken.
2 Die Fourieranalyse findet auch in Gebieten wie der Optik z.B. bei der Analyse von Licht Anwendung, ebenso auch in der Astrophysik zur Berechnung von Rotationszyklen u.v.a.m.
© Klaus Ploch